6-支持向量机

1. 回顾

1.1. 统计学角度看机器学习

机器学习目的得到映射:

• 类先验概率：
• 样本先验概率：
• 类的条件概率：
  • 最大似然估计
• 后验概率：
  • 给出样本，得到类的后验概率，可以判定属于后验概率最高的类

1.2. 统计机器学习方法

1.2.1. 从概率框架

• 生成式模型 Generative models
  • 估计和，然后贝叶斯定理求
• 判别式模型 Discriminative models
  • 直接估计
  • 判别函数 Discriminant fucntion：不假设概率模型，直接求一个把各类分开的边界

2. 感知机

线性超平面：在特征空间可以划分类别

3. 线性支持向量机

3.1. 间隔和支持向量机

• 间隔:一个点对应间隔(margin)式其到分界超平面的垂直距离
• SVM最大化所有训练样本的最小间隔
• 具有最佳间隔的点称为支持向量(support vectors)

3.2. 计算Margin

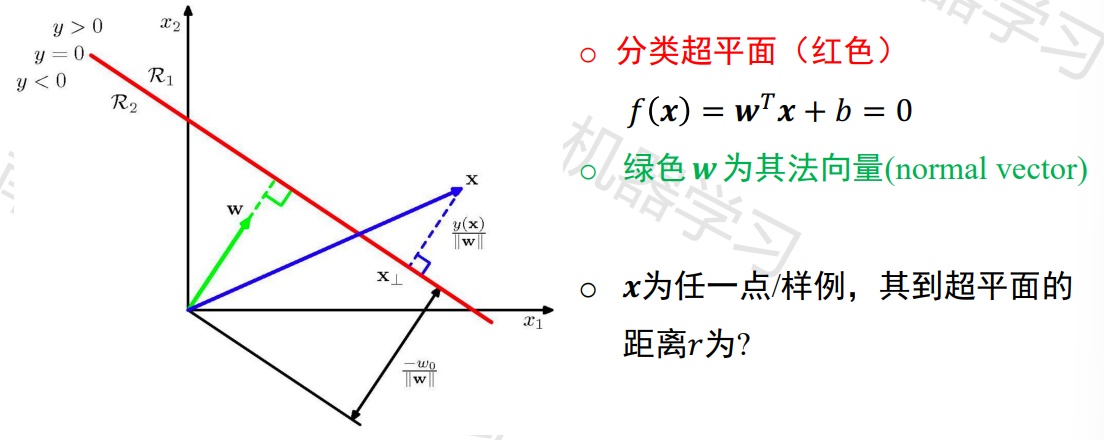
超平面为

• 的投影点为,为距离向量
  • 其方向与相同,为
  • margin为其大小的绝对值
• • , 其中
  • 的margin为

3.3. 分类与评价

• 如何分类

  • 分为正类,分为负类

• 对于任何一个样例,如何判断预测对错? ()

  • 分类正确,分类错误
  • 如果我们假设能完全分开,并且,那么

3.4. SVM形式化描述

• SVM的问题:最大化所有训练样本的最小间隔

• 对没有限制,要求最大化最小间隔,难以优化
• 只需要即可判断是否正确分类
  • 只需要方向,不需要大小
  • 如果变为, 预测和间隔不会变

3.5. 拉格朗日乘子法

把约束条件带到放到目标函数里

3.6. KKT条件

互补松弛性质: 存在拉格朗日乘子后面一项为0时, 优化函数和原始优化函数一致

3.7. Soft margin

允许少量点margin比1小

松弛变量: 允许犯的错误

3.7.1. 如何惩罚

• 原始空间:

: 代价,是我们要最小化的函数
: 正则项, 对分类器进行限制,使得模型的复杂度不要至于太高(还是最大化间隔)
: 超参数, 一般是手工定义

• Soft margin的对偶形式
  • 只依赖于内积

3.8. 总结

#TODO

4. 非线性向量机

4.1. 特征空间映射

• 把样本从原始空间映射到一个更高维空间, 是样本在这个特征空间线性可分
  • 如果原始空间是有限维, 那么一定存在一个高位特征空间使得样本可分

线性和非线性有时是紧密联系在一起–通过内积

4.2. Kernel trick

#TODO

4.3. 限制条件

#TODO

必须存在特征映射, 才可以将非线性函数表示为特征空间中的内积

Mercer’s condition

等价形式:

4.4. 核支持向量机Kernel SVM

核函数:
对偶形式:
边界分类:

4.5. 线性核与非线性核

• 线性核:
• 非线性核
  • RBF/高斯核
  • 多项式核

4.6. 如何选择超参数

用交叉验证在训练集上学习

5. 多类支持向量机

5.1. 1-vs-1

• 思路：转化为2类问题
• C个类别，通过两两组合构造个分类器
• 一共个分类器，其中每个了类出现C-1此
  • 每个分类器使用其二值输出，即
• 对每个样本x，根据结果投票

5.2. 1-vs-all

设计C个分类器，第i个分类器用类i作为正类，其它C-1个作为负类
每个使用其实值输出，即
每个分类器输出可以看作x属于类i的信心

最终输出选择信心最高的那个类